In jedem Messsystem – von der drahtlosen Kommunikation bis zur Digitalfotografie – ist das Signal-Rausch-Verhältnis (SNR) ein grundlegender Qualitätsmaßstab. Ob Sie Teleskopbilder analysieren, Mikrofonaufnahmen verbessern oder eine drahtlose Verbindung beheben, das SNR gibt an, wie viele nützliche Informationen sich von unerwünschtem Hintergrundrauschen abheben.
Die korrekte Berechnung des SNR ist jedoch nicht immer einfach. Je nach System müssen möglicherweise zusätzliche Faktoren wie Dunkelstrom, Leserauschen oder Pixel-Binning berücksichtigt werden. Dieser Leitfaden führt Sie durch die Theorie, die wichtigsten Formeln, häufige Fehler, Anwendungen und praktische Möglichkeiten zur Verbesserung des SNR und stellt sicher, dass Sie ihn in einer Vielzahl von Kontexten präzise anwenden können.
Was ist das Signal-Rausch-Verhältnis (SNR)?
Im Wesentlichen misst das Signal-Rausch-Verhältnis das Verhältnis zwischen der Stärke eines gewünschten Signals und dem Hintergrundrauschen, das es verdeckt.
● Signal = die bedeutungsvolle Information (z. B. eine Stimme bei einem Anruf, ein Stern auf einem Teleskopbild).
● Rauschen = zufällige, unerwünschte Schwankungen, die das Signal verzerren oder verbergen (z. B. statische Aufladung, Sensorrauschen, elektrische Störungen).
Mathematisch wird SNR wie folgt definiert:
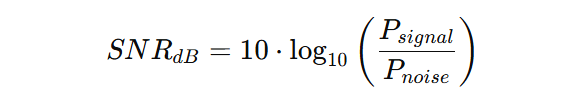
Da diese Verhältnisse um viele Größenordnungen variieren können, wird das SNR üblicherweise in Dezibel (dB) ausgedrückt:
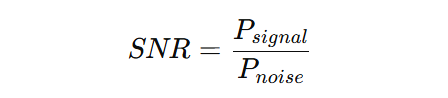
● Hohes SNR (z. B. 40 dB): Das Signal dominiert, was zu klaren und zuverlässigen Informationen führt.
● Niedriges SNR (z. B. 5 dB): Rauschen überlagert das Signal und erschwert die Interpretation.
So berechnen Sie das SNR
Die Berechnung des Signal-Rausch-Verhältnisses kann je nach den einbezogenen Rauschquellen mit unterschiedlicher Genauigkeit durchgeführt werden. In diesem Abschnitt werden zwei Formen vorgestellt: eine, die den Dunkelstrom berücksichtigt, und eine, die davon ausgeht, dass er vernachlässigt werden kann.
Hinweis: Um unabhängige Rauschwerte hinzuzufügen, müssen diese in Quadratur addiert werden. Jede Rauschquelle wird quadriert, summiert und die Quadratwurzel der Summe gezogen.
Signal-Rausch-Verhältnis mit Dunkelstrom
Die folgende Gleichung ist in Situationen zu verwenden, in denen das Dunkelstromrauschen so groß ist, dass es einbezogen werden muss:
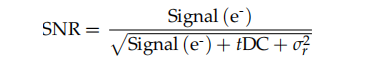
Hier ist die Definition der Begriffe:
Signal (e-): Dies ist das Signal von Interesse in Photoelektronen, wobei das Dunkelstromsignal subtrahiert wird
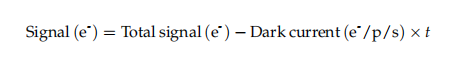
Das Gesamtsignal (e-) ist die Photoelektronenanzahl im betreffenden Pixel – streng genommen nicht der Pixelwert in Graustufen. Die zweite Instanz des Signals (e-), am unteren Ende der Gleichung, ist das Photonenrauschen.
Dunkelstrom (DC):Der Dunkelstromwert für dieses Pixel.
t: Belichtungszeit in Sekunden
σr:Geräusche im Kameramodus lesen.
Signal-Rausch-Verhältnis bei vernachlässigbarem Dunkelstrom
In den Fällen von kurzen (Bei Belichtungszeiten von < 1 Sekunde und gekühlten Hochleistungskameras liegt das Dunkelstromrauschen im Allgemeinen deutlich unter dem Leserauschen und kann problemlos vernachlässigt werden.

Dabei gelten wieder die oben genannten Begriffe, mit der Ausnahme, dass das Dunkelstromsignal nicht berechnet und vom Signal subtrahiert werden muss, da es Null ergeben sollte.
Einschränkungen dieser Formeln und fehlende Begriffe
Die nebenstehenden Formeln liefern nur korrekte Antworten für CCD undCMOS-KamerasEMCCD und verstärkte Geräte führen zusätzliche Rauschquellen ein, daher können diese Gleichungen nicht verwendet werden. Für eine vollständigere Signal-Rausch-Verhältnis-Gleichung, die diese und andere Beiträge berücksichtigt.
Ein weiterer Rauschterm, der häufig in SNR-Gleichungen enthalten ist (oder war), ist die Photo-Response-Non-Uniformity (PRNU), manchmal auch als „Fixed Pattern Noise“ (FPN) bezeichnet. Dies stellt die Ungleichmäßigkeit der Verstärkung und der Signalantwort über den Sensor dar, die bei hohen Signalen dominant werden kann, wenn sie groß genug ist, und so das SNR verringert.
Während frühe Kameras über eine ausreichend große PRNU verfügten, um deren Einbeziehung zu erfordern,wissenschaftliche KamerasDer PRNU-Wert ist ausreichend niedrig, sodass sein Beitrag deutlich unter dem des Photonenrauschens liegt, insbesondere nach Anwendung integrierter Korrekturen. Daher wird er bei SNR-Berechnungen heute meist vernachlässigt. Für einige Kameras und Anwendungen ist der PRNU jedoch weiterhin wichtig und wird der Vollständigkeit halber in die erweiterte SNR-Gleichung einbezogen. Die bereitgestellten Gleichungen sind daher für die meisten CCD/CMOS-Systeme nützlich, sollten aber nicht als universell anwendbar angesehen werden.
Arten von Rauschen in SNR-Berechnungen
Bei der Berechnung des SNR geht es nicht nur darum, ein Signal mit einem einzelnen Rauschwert zu vergleichen. In der Praxis tragen mehrere unabhängige Rauschquellen zum Rauschen bei, und es ist wichtig, sie zu verstehen.
Schrotrauschen
● Ursprung: statistische Ankunft von Photonen oder Elektronen.
● Skaliert mit der Quadratwurzel des Signals.
● Dominant in der photonenlimitierten Bildgebung (Astronomie, Fluoreszenzmikroskopie).
Thermisches Rauschen
● Es wird auch Johnson-Nyquist-Rauschen genannt und durch die Elektronenbewegung in Widerständen erzeugt.
● Steigt mit der Temperatur und Bandbreite.
● Wichtig in der Elektronik und drahtlosen Kommunikation.
Dunkelstromrauschen
● Zufällige Schwankungen des Dunkelstroms in den Sensoren.
● Deutlicher bei langen Belichtungszeiten oder warmen Detektoren.
● Reduziert durch Kühlung des Sensors.
Leserauschen
● Rauschen von Verstärkern und Analog-Digital-Umwandlung.
● Pro Anzeige festgelegt, daher kritisch in Bereichen mit schwachem Signal.
Quantisierungsrauschen
● Durch die Digitalisierung eingeführt (Rundung auf diskrete Ebenen).
● Wichtig bei Systemen mit geringer Bittiefe (z. B. 8-Bit-Audio).
Umgebungs-/Systemgeräusche
● EMI, Übersprechen, Welligkeit der Stromversorgung.
● Kann dominieren, wenn die Abschirmung/Erdung schlecht ist.
Zu wissen, welches dieser Probleme vorherrschend ist, hilft bei der Auswahl der richtigen Formel und Minderungsmethode.
Häufige Fehler bei der Berechnung des SNR
Es gibt viele Abkürzungen zur Schätzung des Signal-Rausch-Verhältnisses in der Bildgebung. Diese sind entweder weniger komplex als die nebenstehenden Gleichungen, ermöglichen eine einfachere Ableitung aus dem Bild selbst, ohne dass Kameraparameter wie das Leserauschen bekannt sein müssen, oder beides. Leider ist jede dieser Methoden wahrscheinlich falsch und führt zu verzerrten und nicht hilfreichen Ergebnissen. Es wird dringend empfohlen, in allen Fällen die nebenstehenden Gleichungen (oder die erweiterte Version) zu verwenden.
Zu den häufigsten falschen Abkürzungen gehören:
1. Vergleich der Signalintensität mit der Hintergrundintensität in Graustufen. Dieser Ansatz versucht, die Kameraempfindlichkeit, die Signalstärke oder das Signal-Rausch-Verhältnis durch den Vergleich einer Spitzenintensität mit einer Hintergrundintensität zu beurteilen. Dieser Ansatz ist jedoch sehr fehlerhaft, da der Einfluss des Kamera-Offsets die Hintergrundintensität beliebig festlegen kann, die Verstärkung die Signalintensität beliebig festlegen kann und der Beitrag von Rauschen im Signal oder Hintergrund nicht berücksichtigt wird.
2. Division der Signalspitzen durch die Standardabweichung eines Bereichs von Hintergrundpixeln. Oder Vergleich der Spitzenwerte mit dem visuellen Rauschen im Hintergrund, das durch ein Linienprofil sichtbar wird. Vorausgesetzt, der Offset wird vor der Division korrekt von den Werten subtrahiert, besteht die größte Gefahr bei diesem Ansatz in der Anwesenheit von Hintergrundlicht. Hintergrundlicht dominiert typischerweise das Rauschen in den Hintergrundpixeln. Darüber hinaus wird das Rauschen im relevanten Signal, wie z. B. Schrotrauschen, überhaupt nicht berücksichtigt.
3. Mittleres Signal in den relevanten Pixeln vs. Standardabweichung der Pixelwerte: Der Vergleich oder die Beobachtung der Veränderung eines Spitzensignals über benachbarte Pixel oder aufeinanderfolgende Frames hinweg ist zwar genauer als andere Abkürzungsmethoden, vermeidet aber wahrscheinlich andere Einflüsse, die die Werte verfälschen, wie z. B. eine Signaländerung, die nicht auf Rauschen zurückzuführen ist. Diese Methode kann aufgrund geringer Pixelzahlen im Vergleich auch ungenau sein. Auch die Subtraktion des Offset-Wertes darf nicht vergessen werden.
4. Berechnung des SNR ohne Umrechnung in Intensitätseinheiten von Photoelektronen oder ohne Entfernen des Offsets: Da das Photonenrauschen typischerweise die größte Rauschquelle darstellt und für die Messung Kenntnisse über den Offset und die Verstärkung der Kamera erforderlich sind, lässt sich die Rückrechnung auf Photoelektronen für die SNR-Berechnung nicht vermeiden.
5. SNR-Beurteilung mit bloßem Auge: Obwohl die visuelle Beurteilung oder der Vergleich des SNR-Verhältnisses in manchen Fällen hilfreich sein kann, birgt sie auch unerwartete Fallstricke. Die Beurteilung des SNR bei Pixeln mit hohem Wert kann schwieriger sein als bei Pixeln mit niedrigem Wert oder Hintergrundpixeln. Auch subtilere Effekte können eine Rolle spielen: Beispielsweise können verschiedene Computermonitore Bilder mit sehr unterschiedlichem Kontrast darstellen. Darüber hinaus kann die Anzeige von Bildern in unterschiedlichen Zoomstufen in der Software die visuelle Darstellung von Rauschen erheblich beeinflussen. Dies ist besonders problematisch beim Vergleich von Kameras mit unterschiedlichen Objektraum-Pixelgrößen. Schließlich kann das Vorhandensein von Hintergrundlicht jede visuelle Beurteilung des SNR-Verhältnisses zunichte machen.
Anwendungen von SNR
SNR ist eine universelle Metrik mit weitreichenden Anwendungen:
● Audio- und Musikaufnahme: Bestimmt Klarheit, Dynamikbereich und Wiedergabetreue von Aufnahmen.
● Drahtlose Kommunikation: SNR steht in direktem Zusammenhang mit der Bitfehlerrate (BER) und dem Datendurchsatz.
● Wissenschaftliche Bildgebung: In der Astronomie ist ein hohes Signal-Rausch-Verhältnis (SNR) erforderlich, um schwache Sterne vor dem Hintergrund des Himmelsleuchtens zu erkennen.
● Medizinische Geräte: EKG-, MRT- und CT-Scans sind auf ein hohes SNR angewiesen, um Signale von physiologischem Rauschen zu unterscheiden.
● Kameras und Fotografie: Sowohl Verbraucherkameras als auch wissenschaftliche CMOS-Sensoren verwenden SNR, um die Leistung bei schwachem Licht zu messen.
Verbesserung des SNR
Da das SNR eine so wichtige Kennzahl ist, wird erheblicher Aufwand in seine Verbesserung gesteckt. Zu den Strategien gehören:
Hardware-Ansätze
● Verwenden Sie bessere Sensoren mit geringerem Dunkelstrom.
● Verwenden Sie eine Abschirmung und Erdung, um elektromagnetische Störungen zu reduzieren.
● Kühlen Sie die Detektoren, um thermisches Rauschen zu unterdrücken.
Software-Ansätze
● Wenden Sie digitale Filter an, um unerwünschte Frequenzen zu entfernen.
● Verwenden Sie die Mittelwertbildung über mehrere Frames.
● Verwenden Sie Rauschunterdrückungsalgorithmen bei der Bild- oder Audioverarbeitung.
Pixel-Binning und seine Auswirkung auf das SNR
Die Auswirkung des Binnings auf das Signal-Rausch-Verhältnis hängt von der Kameratechnologie und dem Sensorverhalten ab, da das Rauschverhalten von Kameras mit und ohne Binning erheblich variieren kann.
CCD-Kameras können die Ladung benachbarter Pixel „on-chip“ summieren. Das Ausleserauschen tritt nur einmal auf, obwohl das Dunkelstromsignal jedes Pixels ebenfalls summiert wird.
Die meisten CMOS-Kameras führen Off-Chip-Binning durch. Das bedeutet, dass die Werte zunächst gemessen (und dabei Leserauschen erzeugt) und dann digital summiert werden. Das Leserauschen bei solchen Summierungen erhöht sich durch Multiplikation mit der Quadratwurzel der Anzahl der summierten Pixel, also um den Faktor 2 beim 2x2-Binning.
Da das Rauschverhalten von Sensoren kompliziert sein kann, empfiehlt es sich für quantitative Anwendungen, den Offset, die Verstärkung und das Lese-Rauschen der Kamera im Binning-Modus zu messen und diese Werte für die Gleichung des Signal-Rausch-Verhältnisses zu verwenden.
Abschluss
Das Signal-Rausch-Verhältnis (SNR) ist eine der wichtigsten Messgrößen in Wissenschaft, Technik und Technologie. Von der Klarheit bei Telefongesprächen bis zur Erkennung entfernter Galaxien ist das SNR entscheidend für die Qualität von Mess- und Kommunikationssystemen. Die Beherrschung des SNR erfordert nicht nur das Auswendiglernen von Formeln, sondern auch das Verständnis von Annahmen, Einschränkungen und realen Kompromissen. Aus dieser Perspektive können Ingenieure und Forscher zuverlässigere Messungen durchführen und Systeme entwickeln, die auch unter lauten Bedingungen aussagekräftige Erkenntnisse liefern.
Möchten Sie mehr erfahren? Schauen Sie sich verwandte Artikel an:
Tucsen Photonics Co., Ltd. Alle Rechte vorbehalten. Bitte geben Sie beim Zitieren die Quelle an:www.tucsen.com

 25.09.11
25.09.11